혼합도, 최종 혼합도
통상의 분립체 혼합조작에 있어 균질의 혼합물이란 (주목한 성분 입자를 발견하는 확률이
혼합물중의 어느 곳에서나 같은 혼합물)이라고 정의한다. 이와 같은 혼합물을 완전 불규칙
혼합물(perfectly random mixture)이라 하고, 또 통계적으로 완전 혼합상태라고
한다. 이와 같이 완전 혼합상태를 정의하면, 혼합물의 균질의 정도, 즉 혼합상태 또는
혼합도(degree of mixing)를 알기 위해 통계학적 수법(추정수법)을 자연히
도입한다. 2성분계(系) 혼합물에서 무작위로 채취한 N개의 스풋 샘플 속의 주목한 성분의
조성 x (i=1,2,...,N)에서 먼저 샘플 평균 xs를 계산한다.
 .....................................................(2.1)
.....................................................(2.1)
裝入 組成 xc를 알고 있을 때 샘플링 조작이 적절하면 xs는 xc와 거의
같아야 하며, 샘플링의 타당성을 조사할 수 있다.
다음에 샘플링의 분산 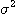 은 다음 2가지로 정의한다.
은 다음 2가지로 정의한다.
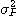 =
= 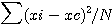 ..........................................(2.2)
..........................................(2.2)
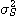 =
= 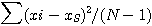 .......................................(2.3)
.......................................(2.3)
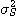 은 모집단의
분산의 자유도
은 모집단의
분산의 자유도  =N 에서의 不偏 추정량이라 부르는 것이다.
=N 에서의 不偏 추정량이라 부르는 것이다. 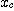 ,
,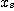 및
및 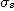 사이에는
사이에는
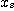 -1.64
-1.64 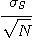
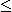
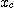
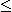
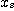 + 1.64
+ 1.64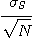 ..........................(2.4)
..........................(2.4)
의 관계가 신뢰성이 90%로 성립한다.따라서 샘플의 분산 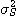 을 측정하면 그 값의 대소에 따라 혼합물의 균질의 정도를 추정할 수 있다. 즉
을 측정하면 그 값의 대소에 따라 혼합물의 균질의 정도를 추정할 수 있다. 즉 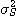 은 혼합도의 한가지 표현이며 실용상으로는 이것으로 충분하다. 그러나
은 혼합도의 한가지 표현이며 실용상으로는 이것으로 충분하다. 그러나 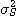 은 여러 가지 측정조건 등의 영향을 받기 때문에 보편적인 척도가 될 수 없다. 그래서
표1-1과 같은 여러 가지 무차원화, 정규화를 제안하고 있다. 이 표의
은 여러 가지 측정조건 등의 영향을 받기 때문에 보편적인 척도가 될 수 없다. 그래서
표1-1과 같은 여러 가지 무차원화, 정규화를 제안하고 있다. 이 표의 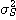 은 완전혼합 상태의 샘플 분산이고, 또
은 완전혼합 상태의 샘플 분산이고, 또 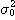 는 완전 분리상태 (혼합하기 전) 에서의 샘플분산이며, 다음식으로 나타낸다
는 완전 분리상태 (혼합하기 전) 에서의 샘플분산이며, 다음식으로 나타낸다
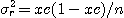 ..................................................(2.5)
..................................................(2.5)
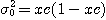 ......................................................(2.6)
......................................................(2.6)
여기서, n은 샘플 싸이즈이며, 1개의 샘플 속에 함유된 분체
입자의 수이다. 표AA에 나타낸 여러 가지 혼합도는 결과적으로는 측정 조건의 영향을 받지
않는 표시방법으로 되어 있으나, 그렇다는 이론적인 보증은 전혀 없으며, 편의적이고, 직관적인
것이다. 다시 말하면, 예를 들어 폐(閉)구간 [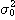 ,
,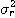 ]을 폐구간
[0,1]에 寫像하여 어느 변(邊)을 확대해서 보느냐가 M의 정의에 따라 변화하는 것에
지나지 않는다. 또 다(多)성분계에 대한 혼합도도 共分散 매트릭스를 사용하여 똑같이 정의할
수 있으나, 계산하는데 노력이 들기 때문에 실용적으로 구성 성분 가운데 가장 중요한 성분(key
component)에 대한 2성분계와 같은 취급을 하는 경우가 많다
]을 폐구간
[0,1]에 寫像하여 어느 변(邊)을 확대해서 보느냐가 M의 정의에 따라 변화하는 것에
지나지 않는다. 또 다(多)성분계에 대한 혼합도도 共分散 매트릭스를 사용하여 똑같이 정의할
수 있으나, 계산하는데 노력이 들기 때문에 실용적으로 구성 성분 가운데 가장 중요한 성분(key
component)에 대한 2성분계와 같은 취급을 하는 경우가 많다
** 대표적인 혼합도의 표시법 **
| 분류 |
혼합도 M의 표현 |
완전혼합Mo |
완전혼합Mr |
| 혼합의 정도를 나타내는것 |
Ⅰ |
1 |
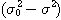 / / 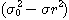 |
0 |
1 |
| 2 |
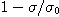 |
0 |
1 |
| Ⅱ |
|
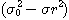 / / 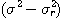 |
1 |
무한대 |
| Ⅲ |
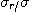 |
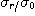 |
1 |
| 미 혼합의 정도를 나타내는것 |
Ⅳ |
1 |
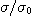 |
1 |
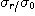 |
| 2 |
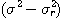 / / 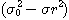 |
1 |
0 |
| Ⅴ |
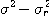 |
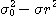 |
0 |
| Ⅵ |
1 |
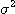 |
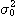 |
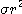 |
| 2 |
 |
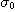 |
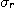 |
回分 혼합에서는 주목한 성분 조성의 공간적인 변동이 문제가 되기 때문에 혼합도에 관한
취급은 위에서 설명한 대로 하면 되나, 연속 혼합에서는 혼합기 출구에서의 주목한 성분
조성의 시간적 변동도 문제가 되므로, 취급 방법이 조금 달라진다. 즉 연속 혼합기에서의
혼합도는 일정한 조작 조건으로 운전중인 혼합기의 출구에서 배출되는 혼합물의 조성 변동의
대소로 나타낼 수 있다. 혼합기의 출구에서 불규칙하거나 일정한 시간간격으로 N조의 샘플을
채취하여, 각각의 조성을 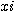 로 하면, 그 시간적 변동의 분산
로 하면, 그 시간적 변동의 분산 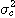 은 회분식의 경우와 마찬가지로 다음 식에서 구한다.
은 회분식의 경우와 마찬가지로 다음 식에서 구한다.
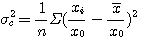 ,
, 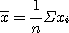 ...........................(2.7)
...........................(2.7)
여기서, 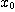 는 입구 조성(혼합비,공급비)이다. 식 (9.8)에서 정의한 혼합도
는 입구 조성(혼합비,공급비)이다. 식 (9.8)에서 정의한 혼합도 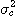 은 정상상태(x,/x0=1.0)에서는 샘플링 시간간격의 영향을 받지 않고, 다른
측정 조건 등의 영향을 실용상 적다는 것이 확인되었다.
은 정상상태(x,/x0=1.0)에서는 샘플링 시간간격의 영향을 받지 않고, 다른
측정 조건 등의 영향을 실용상 적다는 것이 확인되었다.
샘플링 방법 등을 포함한 혼합도의 구체적인 방법에 대해서는 샘플링 해석 참조.
혼합기구
분립체의 혼합은 크게 나누어 다음의 3가지 운동을 수반하여 진행한다.
(1) 이동(對流) 혼합(conventive mixing)
혼합 용기 자체나 교반깃(패들 또는 리번)등의 회전으로, 또는
기류에 의한 추진으로 분체 입자군이 크게 위치를 이동하여, 혼합기 안에서 순환류가 형성되는
것과 같은 운동에 수반하여 생기는 혼합이다. 이 기구는 혼합물 전체의 거시적인 혼합에
크게 기여하고, 속도는 빠르나, 미시적인 혼합의 진행에는 거의 기여하지 않는다. 따라서,
회분 혼합에 대해서는 유익하나, 연속혼합에서는 일반적으로 좋지 않은 영향을 준다.
(2) 전단 혼합(shearing mixing)
분체 입자군 안의 속도 분포로 인해 생기는 입자 상호의 미끄럼(slip)이나
충돌 교반깃의 끝 부분과 용기 벽면 및 밑면 등 사이에서 분립체 集塊가 압축과 신장 등으로
분해되는 작용도 포함한 혼합 작용이다. 용기 회전형 혼합기에서는 경사면으로 흘러내리는
분체층이나 요기의 양 끝에서 나타나고, 또 기류형 혼합기에서는 흡입부분이나 흐름방향의
전환부분에 현저하게 나타낸다. 準徵視的인 혼합에 기여하고, 회분 및 연속혼합의 양자에
바람직한 작용이다.
(3) 확산 혼합(diffusive mixing)
근접한 입자 상호의 위치 교환에 의한 국부적인 혼합을 가리키며, 실제로는
입자의 모양, 충전 상태, 흐름방향의 속도차, 입자의 자전 등에서의 불규칙성에 기인한
이른바, 입자의 醉步(random wallk)로 인해 생기는 작용이다. 용기 회전형에서는
회전축 방향의 혼합이 이에 상당하고, 교반형에서는 깃 등이 직접 통과하지 않는 영역이
상당하고, 또 기류형에서는 플로 패턴이 명확하지 않은 층 상부 등의 혼합이 이에 상당한다.
이동 혼합에 비하여 진행속도는 현저하게 작으나, 조성의 균질화에는 불가결한 미시적인 혼합작용이다.
혼합곡선
실제의 혼합기에서는 앞에 설명한 3가지 혼합기구가 각각의 영역에서 독립하여 일어나는 갓이
아니라, 동시에 작용이 발생하면서 혼합이 진행된다. 혼합이 개시한 때부터 측정한 시간, 즉
혼합시간 t(연속 혼합의 경우는 분립체의 혼합기내 평균체류시간-혼합기내의 분립체의 체적을
체적유량으로 나눈 값)에 대한 혼합도 M의 변화를 플롯한 것을 혼합특성곡선(또는 그냥 혼합곡선)이라
하고, 혼합기의 성능을 표시하는 방법으로서 중요한 것이다. 그림 2-1은 혼합곡선의 일례를
모식적으로 나타낸 것이며,세로축은 샘플의 표준편차  의 대수를 나다냈다. 일반적으로 혼합과정의 초기 구간 I에서는 주로 對流혼합이 지배적이고,
中期 구간Ⅱ에서는 對流와 전단(剪斷)에 의해 정상적으로 혼합이 진행된다. 최종
단계 Ⅲ에서는 확산혼합의 효과가 나타나고,혼합과 분리의 두 작용리 동적 평형상태에 도달한다.
이때의 혼합도를 최종 혼합도
의 대수를 나다냈다. 일반적으로 혼합과정의 초기 구간 I에서는 주로 對流혼합이 지배적이고,
中期 구간Ⅱ에서는 對流와 전단(剪斷)에 의해 정상적으로 혼합이 진행된다. 최종
단계 Ⅲ에서는 확산혼합의 효과가 나타나고,혼합과 분리의 두 작용리 동적 평형상태에 도달한다.
이때의 혼합도를 최종 혼합도 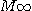 라 한다. 이 그림 2-1의 패턴은 혼합기의 종류에 따라 여러모로 변화한다. 또
라 한다. 이 그림 2-1의 패턴은 혼합기의 종류에 따라 여러모로 변화한다. 또 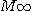 는 조작 조건과 분립체의 물성에 따라 크게 영향을 받는다.
는 조작 조건과 분립체의 물성에 따라 크게 영향을 받는다.
혼합속도
대부분의 혼합기에서도 그림2-1과 같이 혼합의 초기에는 혼합도M의 대수가 시간 t에
대해 직선적으로 변화하는 부분이 있다.이것을 방정식의 형식으로 나타내면 다음 1차 속도과정이
된다.
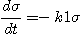 , t=0 과
, t=0 과 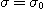 .................. (2.8)
.................. (2.8)
따라서
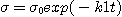 ................................(2.9)
................................(2.9)
또, 표2-1의 (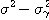 )(
)(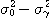 )을
)을
M으로 사용하면
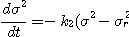 ),t=0과
),t=0과 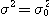 ...........(2.10)
...........(2.10)
따라서
M=exp(-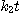 )......................................(2.11)
)......................................(2.11)
이 된다. 이들 식은 어디까지나 현상론적인 표현이고, 본질적인 것은 아니다. 식(9,9)
또는 식 (9,11)의 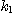 ,
, 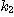 는 그림의 직선부분의 구배이며, 혼합속도계수라 부르며, [1/s]의 차원을 갖는다. 혼합속도계수는
조작 조건과 분립체의 물성에 따라 영향을 받는다.
는 그림의 직선부분의 구배이며, 혼합속도계수라 부르며, [1/s]의 차원을 갖는다. 혼합속도계수는
조작 조건과 분립체의 물성에 따라 영향을 받는다.
인용문헌
1) Timoshenko,S.P.and Goodier,J,N.
: Theory of Elasticity, New York, McGraw-Hill(1951)
2) Rumpf,H. : Beanspruchunstheorie
der Prallzerkleinererung, Chemie-Ing-Techn.,31,5(1959)
3) Farmer,I,W: Engineering Properties
of Rocks, London,E. & F,N SPON(1963)
4) Nakayama J.: Direct Measurement
of Fracture Energies of Brittle Heterogeneous Materials
J.Am.Cer.Soc48,11,(1962)

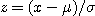 를 적용하여 規準化한 것을 정규분포 또는 規準型 정규분포라 하고,
를 적용하여 規準化한 것을 정규분포 또는 規準型 정규분포라 하고, 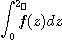 의 값은 함수표에 나타냈다.
의 값은 함수표에 나타냈다. 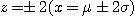 로 둘러싼 면적은 전체의 약 95%이다. 식(1.1)의 파라미터 및
로 둘러싼 면적은 전체의 약 95%이다. 식(1.1)의 파라미터 및 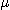 및
및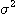 은 일반적으로 未知이므로, 다음의 표본평균, 표본분산을 적용하여 각각 추정한다.
은 일반적으로 未知이므로, 다음의 표본평균, 표본분산을 적용하여 각각 추정한다.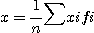 ........................................(1.2)
........................................(1.2)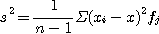 .............................(1.3a)
.............................(1.3a)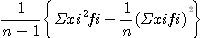 ................(1.3b)
................(1.3b)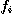 는 계급으로 분할하였을 때 얻는 度數이다.
는 계급으로 분할하였을 때 얻는 度數이다.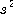 이 不偏 분산이 되도록 하기 위한 것이며, 표본의 크기(sample size)n이 1에 비하여
크면 문제가 되지 않는다. 표본 분산의 평방근을 표본 표준편차라 한다.
이 不偏 분산이 되도록 하기 위한 것이며, 표본의 크기(sample size)n이 1에 비하여
크면 문제가 되지 않는다. 표본 분산의 평방근을 표본 표준편차라 한다.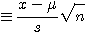 .........................................................(1.4)
.........................................................(1.4)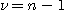 의t 분포에 따르는 점에서 다음 식이 된다.
의t 분포에 따르는 점에서 다음 식이 된다.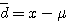 를 편차라 한다.
를 편차라 한다.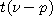 는 數表로 나타냈으며, 그 일부를 표1-1에 나타냈다. 식(4.5)의 t는 신뢰도(1-p)에서
는 數表로 나타냈으며, 그 일부를 표1-1에 나타냈다. 식(4.5)의 t는 신뢰도(1-p)에서 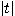 <
<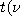 , p)로 된다.
, p)로 된다.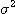 의 신뢰도(1-p)의 신뢰 구간은
의 신뢰도(1-p)의 신뢰 구간은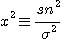 ..............................................................(1.5)
..............................................................(1.5)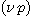
 의
의 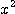 분포에 따르는 점에서 다음식이 된다.
분포에 따르는 점에서 다음식이 된다.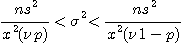 .........................................(1.6)
.........................................(1.6)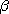 를
를 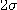 사용하여 나타낸다. 정밀도는 정밀함과 정확함의 양자 또는 어느 한쪽을 말하나, 일반적으로 정밀함을
정밀도라 이르는 경우가 많다. 표준편차
사용하여 나타낸다. 정밀도는 정밀함과 정확함의 양자 또는 어느 한쪽을 말하나, 일반적으로 정밀함을
정밀도라 이르는 경우가 많다. 표준편차  를 평균오차라 하고, (2.3)
를 평균오차라 하고, (2.3) 를 公算 오차라 하며, 정밀함을 나타내는데 사용하고 이밖에 다음과 같은 변동계수(coefficient of variation)를 많이 사용한다.
를 公算 오차라 하며, 정밀함을 나타내는데 사용하고 이밖에 다음과 같은 변동계수(coefficient of variation)를 많이 사용한다.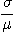 x100%
x100%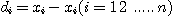 를 구한다.
를 구한다. 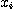 는 바른 방법으로 얻은 데이터(예, 질량 中位지름),
는 바른 방법으로 얻은 데이터(예, 질량 中位지름), 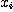 는 대상으로 하는 방법에 의한 데이터.
는 대상으로 하는 방법에 의한 데이터.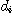 의 不偏 분산
의 不偏 분산 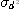 을 구한다.(단(1.3b)와 유사한 식)
을 구한다.(단(1.3b)와 유사한 식) 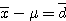 )
)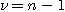 , 有意 수준 5%(p=0.05)에 대한 t(
, 有意 수준 5%(p=0.05)에 대한 t( ,0.05)를 구한다.
,0.05)를 구한다. ,0.05)를 비교하여
,0.05)를 비교하여 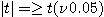 이면 비교 대상으로 하는 간편법에는 치우침(편차)이 있다고 판정한다. 치우침(편차)의 크기는
이면 비교 대상으로 하는 간편법에는 치우침(편차)이 있다고 판정한다. 치우침(편차)의 크기는 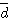 로 나타낸다.
로 나타낸다.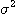 은 다음 2가지로 정의한다.
은 다음 2가지로 정의한다.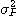 =
= 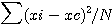 ..........................................(2.2)
..........................................(2.2)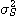 =
= 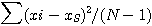 .......................................(2.3)
.......................................(2.3)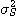 은 모집단의
분산의 자유도
은 모집단의
분산의 자유도  =N 에서의 不偏 추정량이라 부르는 것이다.
=N 에서의 不偏 추정량이라 부르는 것이다. 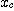 ,
,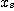 및
및 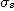 사이에는
사이에는 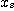 -1.64
-1.64 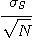
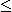
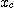
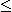
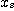 + 1.64
+ 1.64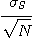 ..........................(2.4)
..........................(2.4)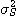 을 측정하면 그 값의 대소에 따라 혼합물의 균질의 정도를 추정할 수 있다. 즉
을 측정하면 그 값의 대소에 따라 혼합물의 균질의 정도를 추정할 수 있다. 즉 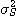 은 혼합도의 한가지 표현이며 실용상으로는 이것으로 충분하다. 그러나
은 혼합도의 한가지 표현이며 실용상으로는 이것으로 충분하다. 그러나 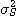 은 여러 가지 측정조건 등의 영향을 받기 때문에 보편적인 척도가 될 수 없다. 그래서
표1-1과 같은 여러 가지 무차원화, 정규화를 제안하고 있다. 이 표의
은 여러 가지 측정조건 등의 영향을 받기 때문에 보편적인 척도가 될 수 없다. 그래서
표1-1과 같은 여러 가지 무차원화, 정규화를 제안하고 있다. 이 표의 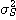 은 완전혼합 상태의 샘플 분산이고, 또
은 완전혼합 상태의 샘플 분산이고, 또 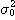 는 완전 분리상태 (혼합하기 전) 에서의 샘플분산이며, 다음식으로 나타낸다
는 완전 분리상태 (혼합하기 전) 에서의 샘플분산이며, 다음식으로 나타낸다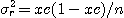 ..................................................(2.5)
..................................................(2.5)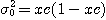 ......................................................(2.6)
......................................................(2.6)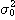 ,
,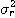 ]을 폐구간
[0,1]에 寫像하여 어느 변(邊)을 확대해서 보느냐가 M의 정의에 따라 변화하는 것에
지나지 않는다. 또 다(多)성분계에 대한 혼합도도 共分散 매트릭스를 사용하여 똑같이 정의할
수 있으나, 계산하는데 노력이 들기 때문에 실용적으로 구성 성분 가운데 가장 중요한 성분(key
component)에 대한 2성분계와 같은 취급을 하는 경우가 많다
]을 폐구간
[0,1]에 寫像하여 어느 변(邊)을 확대해서 보느냐가 M의 정의에 따라 변화하는 것에
지나지 않는다. 또 다(多)성분계에 대한 혼합도도 共分散 매트릭스를 사용하여 똑같이 정의할
수 있으나, 계산하는데 노력이 들기 때문에 실용적으로 구성 성분 가운데 가장 중요한 성분(key
component)에 대한 2성분계와 같은 취급을 하는 경우가 많다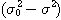 /
/ 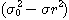
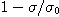
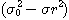 /
/ 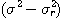
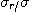
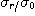
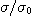
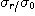
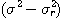 /
/ 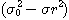
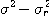
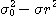
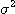
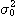
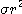

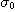
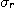
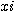 로 하면, 그 시간적 변동의 분산
로 하면, 그 시간적 변동의 분산 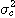 은 회분식의 경우와 마찬가지로 다음 식에서 구한다.
은 회분식의 경우와 마찬가지로 다음 식에서 구한다.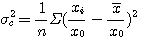 ,
, 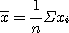 ...........................(2.7)
...........................(2.7)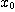 는 입구 조성(혼합비,공급비)이다. 식 (9.8)에서 정의한 혼합도
는 입구 조성(혼합비,공급비)이다. 식 (9.8)에서 정의한 혼합도 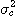 은 정상상태(x,/x0=1.0)에서는 샘플링 시간간격의 영향을 받지 않고, 다른
측정 조건 등의 영향을 실용상 적다는 것이 확인되었다.
은 정상상태(x,/x0=1.0)에서는 샘플링 시간간격의 영향을 받지 않고, 다른
측정 조건 등의 영향을 실용상 적다는 것이 확인되었다. 의 대수를 나다냈다. 일반적으로 혼합과정의 초기 구간 I에서는 주로 對流혼합이 지배적이고,
中期 구간Ⅱ에서는 對流와 전단(剪斷)에 의해 정상적으로 혼합이 진행된다. 최종
단계 Ⅲ에서는 확산혼합의 효과가 나타나고,혼합과 분리의 두 작용리 동적 평형상태에 도달한다.
이때의 혼합도를 최종 혼합도
의 대수를 나다냈다. 일반적으로 혼합과정의 초기 구간 I에서는 주로 對流혼합이 지배적이고,
中期 구간Ⅱ에서는 對流와 전단(剪斷)에 의해 정상적으로 혼합이 진행된다. 최종
단계 Ⅲ에서는 확산혼합의 효과가 나타나고,혼합과 분리의 두 작용리 동적 평형상태에 도달한다.
이때의 혼합도를 최종 혼합도 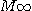 라 한다. 이 그림 2-1의 패턴은 혼합기의 종류에 따라 여러모로 변화한다. 또
라 한다. 이 그림 2-1의 패턴은 혼합기의 종류에 따라 여러모로 변화한다. 또 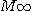 는 조작 조건과 분립체의 물성에 따라 크게 영향을 받는다.
는 조작 조건과 분립체의 물성에 따라 크게 영향을 받는다.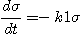 , t=0 과
, t=0 과 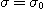 .................. (2.8)
.................. (2.8)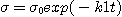 ................................(2.9)
................................(2.9)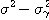 )(
)(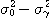 )을
)을 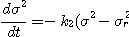 ),t=0과
),t=0과 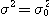 ...........(2.10)
...........(2.10)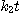 )......................................(2.11)
)......................................(2.11)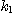 ,
, 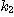 는 그림의 직선부분의 구배이며, 혼합속도계수라 부르며, [1/s]의 차원을 갖는다. 혼합속도계수는
조작 조건과 분립체의 물성에 따라 영향을 받는다.
는 그림의 직선부분의 구배이며, 혼합속도계수라 부르며, [1/s]의 차원을 갖는다. 혼합속도계수는
조작 조건과 분립체의 물성에 따라 영향을 받는다.